11sci

Newton's theory of gravitation[edit]

Main article: Newton's law of universal gravitation

Sir Isaac Newton, an English physicist who lived from 1642 to 1727

In 1687, English mathematician Sir Isaac Newton published Principia, which hypothesizes the inverse-square law of universal gravitation. In his own words, "I deduced that the forces which keep the planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly."^[6] The equation is the following:

F=G{\frac {m_{1}m_{2}}{r^{2}}}\

Where F is the force, m₁ and m₂ are the masses of the objects interacting, r is the distance between the centers of the masses and G is thegravitational constant.

Newton's theory enjoyed its greatest success when it was used to predict the existence of Neptune based on motions of Uranus that could not be accounted for by the actions of the other planets. Calculations by both John Couch Adams and Urbain Le Verrier predicted the general position of the planet, and Le Verrier's calculations are what led Johann Gottfried Galle to the discovery of Neptune.

A discrepancy in Mercury's orbit pointed out flaws in Newton's theory. By the end of the 19th century, it was known that its orbit showed slight perturbations that could not be accounted for entirely under Newton's theory, but all searches for another perturbing body (such as a planet orbiting the Sun even closer than Mercury) had been fruitless. The issue was resolved in 1915 by Albert Einstein's new theory of general relativity, which accounted for the small discrepancy in Mercury's orbit.

Although Newton's theory has been superseded by the Einstein's general relativity, most modern non-relativistic gravitational calculations are still made using Newton's theory because it is simpler to work with and it gives sufficiently accurate results for most applications involving sufficiently small masses, speeds and energies.

Equivalence principle[edit]

The equivalence principle, explored by a succession of researchers including Galileo, Loránd Eötvös, and Einstein, expresses the idea that all objects fall in the same way, and that the effects of gravity are indistinguishable from certain aspects of acceleration and deceleration. The simplest way to test the weak equivalence principle is to drop two objects of different masses or compositions in a vacuum and see whether they hit the ground at the same time. Such experiments demonstrate that all objects fall at the same rate when other forces (such as air resistance and electromagnetic effects) are negligible. More sophisticated tests use a torsion balance of a type invented by Eötvös. Satellite experiments, for example STEP, are planned for more accurate experiments in space.^[7]

Formulations of the equivalence principle include:

The weak equivalence principle: The trajectory of a point mass in a gravitational field depends only on its initial position and velocity, and is independent of its composition.^[8]
The Einsteinian equivalence principle: The outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its location in spacetime.^[9]
The strong equivalence principle requiring both of the above.

General relativity[edit]

Two-dimensional analogy of spacetime distortion generated by the mass of an object. Matter changes the geometry of spacetime, this (curved) geometry being interpreted as gravity. White lines do not represent the curvature of space but instead represent the coordinate system imposed on the curved spacetime, which would be rectilinear in a flat spacetime.

General relativity
$G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }$ $G_{\mu \nu }+\Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }$
Introduction History Mathematical formulation Tests
Fundamental concepts[show]
Phenomena[show]
Equations Formalisms [show]
Solutions [show]
Scientists[show]
v t e

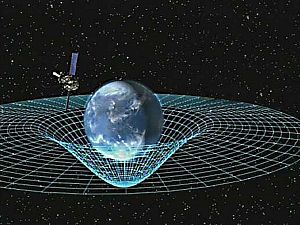
In general relativity, the effects of gravitation are ascribed to spacetime curvature instead of a force. The starting point for general relativity is the equivalence principle, which equates free fall with inertial motion and describes free-falling inertial objects as being accelerated relative to non-inertial observers on the ground.^[10]^[11] In Newtonian physics, however, no such acceleration can occur unless at least one of the objects is being operated on by a force.

Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. These straight paths are called geodesics. Like Newton's first law of motion, Einstein's theory states that if a force is applied on an object, it would deviate from a geodesic. For instance, we are no longer following geodesics while standing because the mechanical resistance of the Earth exerts an upward force on us, and we are non-inertial on the ground as a result. This explains why moving along the geodesics in spacetime is considered inertial.

Einstein discovered the field equations of general relativity, which relate the presence of matter and the curvature of spacetime and are named after him. The Einstein field equations are a set of 10 simultaneous, non-linear, differential equations. The solutions of the field equations are the components of the metric tensor of spacetime. A metric tensor describes a geometry of spacetime. The geodesic paths for a spacetime are calculated from the metric tensor.

Solutions[edit]

Notable solutions of the Einstein field equations include:

The Schwarzschild solution, which describes spacetime surrounding a spherically symmetric non-rotating uncharged massive object. For compact enough objects, this solution generated a black hole with a central singularity. For radial distances from the center which are much greater than the Schwarzschild radius, the accelerations predicted by the Schwarzschild solution are practically identical to those predicted by Newton's theory of gravity.
The Reissner-Nordström solution, in which the central object has an electrical charge. For charges with a geometrized length which are less than the geometrized length of the mass of the object, this solution produces black holes with double event horizons.
The Kerr solution for rotating massive objects. This solution also produces black holes with multiple event horizons.
The Kerr-Newman solution for charged, rotating massive objects. This solution also produces black holes with multiple event horizons.
The cosmological Friedmann-Lemaître-Robertson-Walker solution, which predicts the expansion of the Universe.

Tests[edit]

The tests of general relativity included the following:^[12]

General relativity accounts for the anomalous perihelion precession of Mercury.^[13]
The prediction that time runs slower at lower potentials (gravitational time dilation) has been confirmed by the Pound–Rebka experiment (1959), the Hafele–Keating experiment, and the GPS.
The prediction of the deflection of light was first confirmed by Arthur Stanley Eddington from his observations during the Solar eclipse of May 29, 1919.^[14]^[15] Eddington measured starlight deflections twice those predicted by Newtonian corpuscular theory, in accordance with the predictions of general relativity. However, his interpretation of the results was later disputed.^[16] More recent tests using radio interferometric measurements of quasars passing behind the Sun have more accurately and consistently confirmed the deflection of light to the degree predicted by general relativity.^[17] See also gravitational lens.
The time delay of light passing close to a massive object was first identified by Irwin I. Shapiro in 1964 in interplanetary spacecraft signals.
Gravitational radiation has been indirectly confirmed through studies of binary pulsars. On 11 February 2016, the LIGO and Virgo collaborations announced the first observation of a gravitational wave.
Alexander Friedmann in 1922 found that Einstein equations have non-stationary solutions (even in the presence of the cosmological constant). In 1927 Georges Lemaîtreshowed that static solutions of the Einstein equations, which are possible in the presence of the cosmological constant, are unstable, and therefore the static Universe envisioned by Einstein could not exist. Later, in 1931, Einstein himself agreed with the results of Friedmann and Lemaître. Thus general relativity predicted that the Universe had to be non-static—it had to either expand or contract. The expansion of the Universe discovered by Edwin Hubble in 1929 confirmed this prediction.^[18]
The theory's prediction of frame dragging was consistent with the recent Gravity Probe B results.^[19]
General relativity predicts that light should lose its energy when traveling away from massive bodies through gravitational redshift. This was verified on earth and in the solar system around 1960.